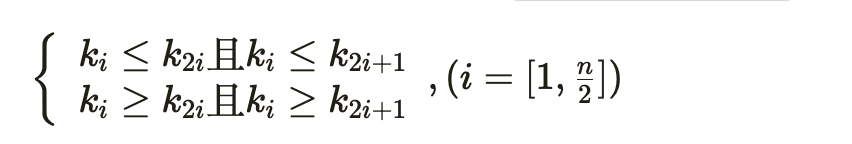container/heap包使用指南
Categories:
本文基于官方文档介绍 golang 标准库中提供的堆/优先队列的使用方法.
1. 概述
“container/heap” 包提供了实现堆操作的接口,用户只需要定义满足 “heap.Interface” 接口的类型,就可以通过包提供的函数,像操作大根堆或小根堆一样,对实例数组变量进行 Push 和 Pop 操作。
堆通常是一个可以被看做一棵树的数组对象,堆总是满足下列性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树。
堆的定义如下:n 个元素的序列 {k1,k2,ki,…,kn} 当且仅当满足下关系时,称之为堆:
下面将基于具体实例介绍"container/heap" 包的使用。
2. 整数堆
下面的代码实现了一个整数类型的最小堆:
package main
import (
"container/heap"
"log"
)
type IntHeap []int
// 下面几个函数必须实现,heap包会进行回调
func (h IntHeap) Len() int { return len(h) }
// Less函数的实现决定最终实现是最大堆还是最小堆
func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
func (h IntHeap) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *IntHeap) Push(x any) { *h = append((*h), x.(int)) }
func (h *IntHeap) Pop() any {
old := *h
n := len(old)
x := old[n-1]
*h = old[0 : n-1]
return x
}
func main() {
h := &IntHeap{2, 1, 5}
heap.Init(h)
heap.Push(h, 3)
log.Println(*h)
for h.Len() > 0 {
log.Println(heap.Pop(h))
}
}
3. 标准库堆的实现
通过整数堆的使用方式,发现是通过定义新的整数数组类型,并为其实现 pointer receivers 的方法 Push、Pop,以及 value receivers 的方法 Len、Less、Swap 方法之后,借助 “container/heap” 包提供的方法对该类型定义的几个方法进行回调,从而实现堆的功能。下面是具体的实现代码,逻辑见注释:
package heap
import "sort"
// Interface 接口指明了想要使用这个包中的方法去实现堆,应该提供的接口方法
// 在 heap.Init 方法被调用、数据为空或者原始数据有序时,满足下列条件的情况下,小根堆会被建立
// !h.Less(j, i) for 0 <= i < h.Len() and 2*i+1 <= j <= 2*i+2 and j < h.Len()
// 注意:包中的方法会在添加和删除元素的时候调用Interface 接口实现的 Push 和 Pop方法,详见下面代码
type Interface interface {
sort.Interface // 包括 Len()、Less(i, j int)、Swap(i, j int)
Push(x any) // add x as element Len()
Pop() any // remove and return element Len() - 1.
}
// 将传入的变量初始化为堆,时间复杂度为 O(n), 其中 n = h.Len().
func Init(h Interface) {
// heapify
n := h.Len()
for i := n/2 - 1; i >= 0; i-- {
down(h, i, n)
}
}
// 向堆中加入新的元素,时间复杂度为 O(log n), 其中 n = h.Len().
func Push(h Interface, x any) {
h.Push(x)
up(h, h.Len()-1)
}
// Pop 移除并返回堆中的最小或最大元素,具体根据 h.Less 函数确定,时间复杂度为 O(log n).
// Pop 等价于 Remove(h, 0).
func Pop(h Interface) any {
n := h.Len() - 1
h.Swap(0, n)
down(h, 0, n)
// 由此看出实现 h.Pop 方法时只需要将数组最后元素取出并返回即可
return h.Pop()
}
// Remove 移除并返回堆中索引为 i 的元素,时间复杂度为 O(log n).
func Remove(h Interface, i int) any {
n := h.Len() - 1
if n != i {
h.Swap(i, n)
if !down(h, i, n) {
up(h, i)
}
}
return h.Pop()
}
// 当堆数组中索引 i 处的元素的值或优先级发生变更的时候调用 Fix 调整元素 i 在堆中的位置
func Fix(h Interface, i int) {
if !down(h, i, h.Len()) {
up(h, i)
}
}
// 向上进行堆调整,将新增元素上升到满足条件的位置
func up(h Interface, j int) {
for {
i := (j - 1) / 2 // parent
if i == j || !h.Less(j, i) {
break
}
h.Swap(i, j)
j = i
}
}
// 向下进行堆调整,确保i0节点是左右子树中的最小节点
func down(h Interface, i0, n int) bool {
i := i0
for {
j1 := 2*i + 1
if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
break
}
j := j1 // left child
if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
j = j2 // = 2*i + 2 // right child
}
if !h.Less(j, i) {
break
}
h.Swap(i, j)
i = j
}
return i > i0
}
4. 优先队列
举例实现针对结构实现的最小堆,也即一般意义上的优先队列:
package main
import (
"container/heap"
"log"
)
type Node struct {
Val int
Next float32
}
type NodeHeap []Node
func (pq NodeHeap) Less(i, j int) bool { return pq[i].Val < pq[j].Val }
func (pq NodeHeap) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
func (pq NodeHeap) Len() int { return len(pq) }
func (pq *NodeHeap) Push(x any) { *pq = append(*pq, x.(Node)) }
func (pq *NodeHeap) Pop() any {
old := *pq
n := len(old)
x := old[n-1]
*pq = old[0 : n-1]
return x
}
func main() {
pq := &NodeHeap{}
heap.Init(pq)
heap.Push(pq, Node{Val: 10, Next: 1.0})
heap.Push(pq, Node{Val: 11, Next: 2.0})
heap.Push(pq, Node{Val: 1, Next: 3.0})
for pq.Len() > 0 {
log.Println(heap.Pop(pq).(Node))
}
}
5. 优先队列的应用
力扣第 23 题「 合并 K 个升序链表」,要求合并 k 个有序链表为 1 个有序列表,如何快速得到 k 个节点中的最小节点,接到结果链表上?
此时就可以使用上述实现的优先队列了,不过需要稍微改动一下结构体,实现如下:
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
type ItemHeap []*ListNode
func (pq ItemHeap) Less(i, j int) bool { return pq[i].Val < pq[j].Val}
func (pq ItemHeap) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]}
func (pq ItemHeap) Len() int {return len(pq)}
func (pq *ItemHeap) Push(x interface{}) { *pq = append(*pq, x.(*ListNode)) }
func (pq *ItemHeap) Pop() interface{} {
old := *pq
n := len(old)
x := old[n-1]
*pq = old[0:n-1]
return x
}
func mergeKLists(lists []*ListNode) *ListNode {
pq := &ItemHeap{}
heap.Init(pq)
for _, v := range lists {
if v != nil {
heap.Push(pq, v)
}
}
// dummy
dummy := &ListNode{}
p := dummy
for pq.Len() > 0 {
x := heap.Pop(pq).(*ListNode)
p.Next = x
p = p.Next
if x.Next != nil {
heap.Push(pq, x.Next)
}
}
return dummy.Next
}